I recently stumbled across a post about a very unique formula called Tupper’s self-referential formula. This formula allows you to plot anything that can fit into a 106 wide by 17 tall grid. It is called “self-referential” because this formula can plot itself on the grid.
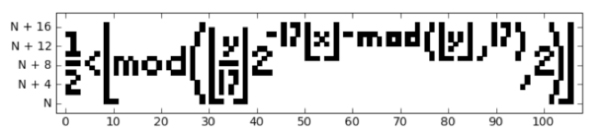
An easier to read version of the formula is:
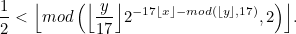
Don’t worry if these seems like a bit of a Frankenstein’s Monster of a formula, there is a rather intuitive understanding behind it.
- We can take everything on the right had side of the ‘<‘ sign and wrap it all up as a function f(x,y). This function takes in two values x, y that represent a square on the 106×17 grid I was talking about earlier.
- This function will then spit out a value (calculated using the big formula above), which we will then compare to 1/2.
- If the value that we get from f(x,y) is greater then 1/2, we color in the box on the grid that is represented by x and y.
- If the value we get is less than, or equal to 1/2, we don’t color in the box, and leave it blank.
- This process is done (by a computer) for every single x and y value that we want to look at.
Now in order to find the bit of the output graph that produces the image we want, we have to find the point on the y-axis where this image starts. In the diagram above, this is shown as the number N. There is another function to find the point where your desired image will start, but it would require another lengthy explanation, so I shall leave it out here. Skipping over the method for finding this, if we start graphing at the number below, we will end up with the image of the formula above.
960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719
This 543-digit monstrosity can be thought of as the unique code for the image of the formula. The really cool part of Tupper’s formula is that you can create any image, provided that you can fit it into a 106×17 grid. In fact, the formula generates every single possible image that can fit into that 106×17 grid, and all we have to do is find the point at which the image we want starts. I find this fascinating, as literally any piece of information can be encoded with this formula.
Using the tool at https://keelyhill.github.io/tuppers-formula/, I made my own message that a reader can find by plugging in the number below:
3001547358332770337372193127007941112227917925519022078304465383983124232533144561341576011711896582837921994365782183448232289052064015773896436007050360698547286909389057858213997522549096288462346206978648063732239023943282643481174067982217989028008850820503895735538113981777002133004132473920044226681146756708625935883057578117674089671844674436952927335276076991889638741656026059567568222136535872544438084795695231639874783784523382786606698519481516815942858219600715039048293001724370495587956592344214989611120887362466985852010496
Finally, my source for this post is available at the starting location of
7845537408904881636064106214019549300205215619222485587018701716195646432344602803459114735925011308779228667093471850927255552811045168928997859454200967078070417294338953745932718753239778710955582001217046244805771391630460355923564278851978862601434046077680409660655269354118985326403017298859607638517927118207761770809581559261192095313776776095699605690678663027578532917535666203037284366066187987963206072697970534845667420812876428909190113491880948688243554409272615443199691039313055326933942373971918848
